Averaging weights leads to wider optima and better generalization

Abstract

Deep neural networks are typically trained by optimizing a loss function with a Stochastic Gradient Descent (SGD) variant, in conjunction with a decaying learning rate, until convergence. We show that simple averaging of multiple points along the trajectory of SGD, with a cyclical or constant learning rate, leads to better generalization than conventional training. We also show that this Stochastic Weight Averaging (SWA) procedure finds much flatter solutions than SGD, is extremely easy to implement, improves generalization, and has almost no computational overhead.

Key takeaways

• Averaging the weights of multiple points along the trajectory of SGD with a cyclical or constant learning rate leads to better generalization than conventional training with a decaying learning rate.
• SWA procedure finds flatter solutions in the loss landscape than SGD, indicating a wider region of optimal weights, which is associated with better generalization.
• SWA can be seen as an approximation of Fast Geometric Ensembling (FGE), achieving comparable performance with a single model.
• SWA is simple to implement, has minimal computational overhead, and significantly improves test accuracy across various architectures and datasets, including CIFAR and ImageNet.
• Improvements in generalization are relatively small.

Experiment

Preliminary concepts

• Hypothesis : weights of the networks ensembled by FGE are on the periphery of the most desirable solutions. It suggests it is promising to average these points in weight space, and use a network with these averaged weights, instead of forming an ensemble by averaging the outputs of networks in model space, to keep the test-time, convenience and interpretability of a single model.
• Conjecture : the width of the optima is critically related to generalization. The general explanation for the importance of width is that the surfaces of train loss and test error are shifted with respect to each other and it is thus desirable to converge to the modes of broad optima, which stay approximately optimal under small perturbations.

Objectives

SGD typically finds points on the periphery of a set of good weights. By running SGD with a cyclical or high constant learning rate, we traverse the surface of this set of points, and by averaging we find a more centred solution in a flatter region of the training loss.

Setup

• Tested architectures: VGG-16, Preactivation ResNet-164, Wide ResNet-28-10, Shake-Shake-2x64d, PyramidNet-272, ResNet-50, ResNet-152, and DenseNet-161.
• Datasets: CIFAR-10, CIFAR-100, and ImageNet ILSVRC-2012.
• Cyclical learning rate : in each cycle $c$ we linearly decrease the learning rate from ${\alpha }_1$ to ${\alpha }_2$, hence the learning rate $\alpha (i)$ at batch iteration $i$:

$\alpha (i)=(1-t(i)){\alpha }_1+t(i){\alpha }_2$

$t(i)=\frac{1}{c}(\text{mod}(i-1,c)+1)$

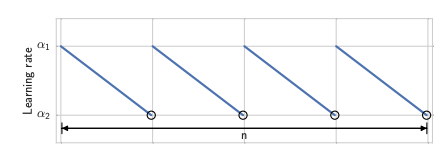
• Initializing SWA with a model pretrained using conventional SGD, potentially with a reduced number of epochs.
• The primary evaluation metric is test accuracy. The study also analyzes train loss to understand the geometry of the loss surface.
• SWA Algorithm:
  • start with a pretrained model $\hat{w}$ (typically early stopping on budget)
  • continue training using a cyclical or constant learning rate
  • capture the models $w_i$ that correspond to the minimum values of the learning rate
  • average the weights of all the captured networks $w_i$ to get final model $w_{SWA}$.

Results

• Use the first, middle and last point of each of the trajectories to define a 2-dimensional plane in the weight space containing all affine combinations of these points. The trajectories do not generally lie in the plane of the plot, except for the first, last and middle points, showed by black crosses in the figure. Therefore for other points of the trajectories it is not possible to tell the value of train loss and test error from the plots. 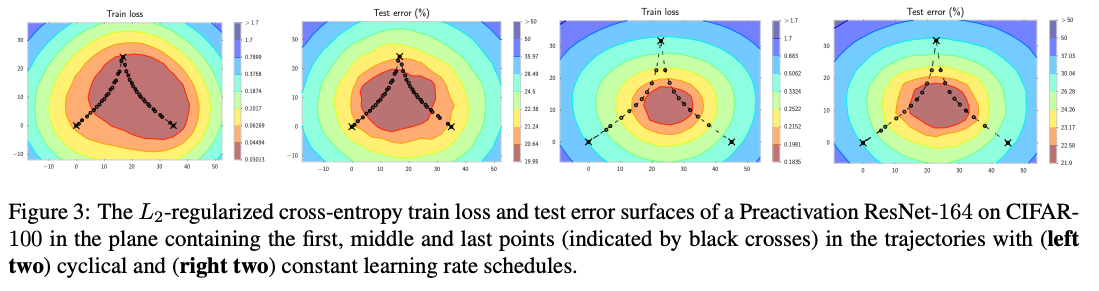→ Both methods explore points close to the periphery of the set of high-performing networks.

• Start from final models $w_{SWA}$ and $w_{SGD}$, draw random directions and follow their paths while evaluating test error and train loss. 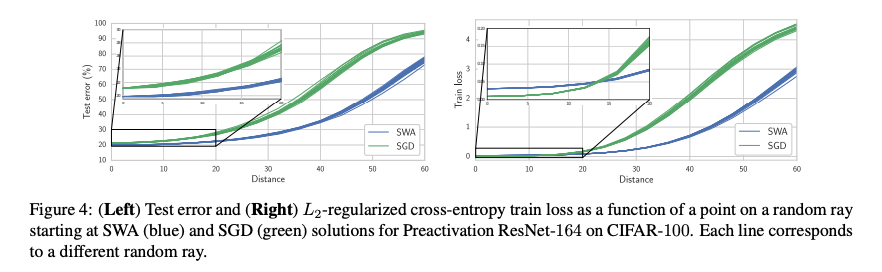→ any of the random directions from $w_{SGD}$ increase test error, while $w_{SWA}$ is much flatter.

• Now consider the path from 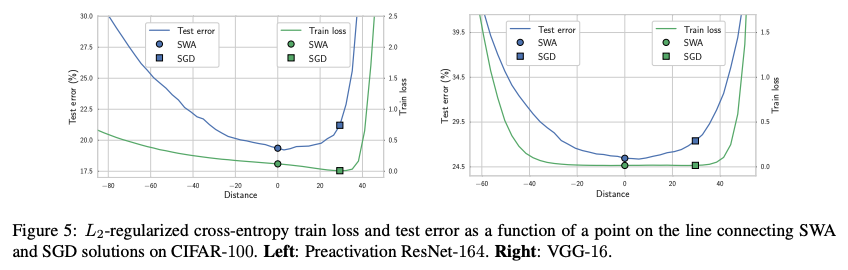$w_{SGD}$ to $w_{SWA}$ → train loss and test error plots are indeed substantially shifted.

→ the point obtained by minimizing the train loss is far from optimal on test.

→ the loss is very steep near $w_{SGD}$.