Automata-based constraints for language model decoding

Abstract

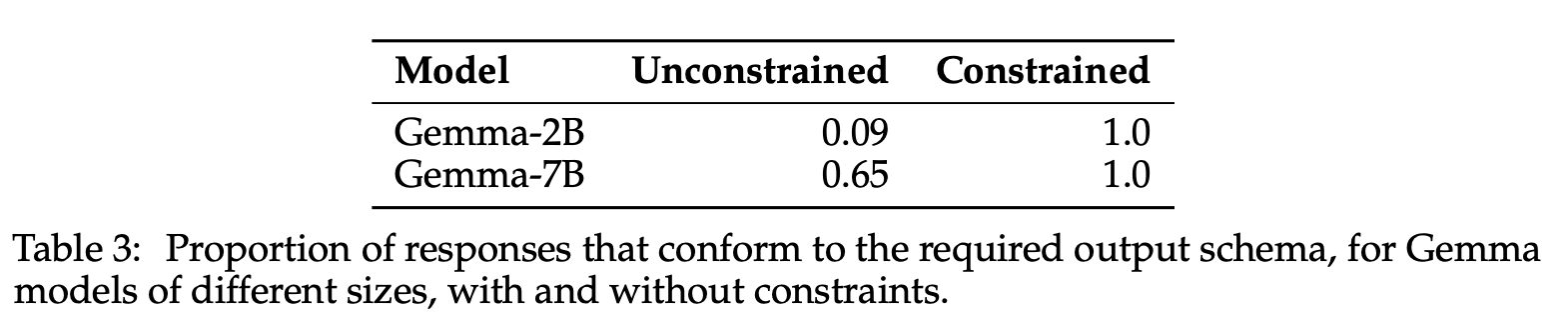
Language models are often expected to generate strings in some formal language; for example, structured data, API calls, or code snippets. Although LMs can be tuned to improve their adherence to formal syntax, this does not guarantee conformance. In addition, tuning requires significant resources, making it impractical for uncommon or task-specific formats. To prevent downstream parsing errors we would ideally constrain the LM to only produce valid output, but this is severely complicated by tokenization, which is typically both ambiguous and misaligned with the formal grammar. We solve these issues through the application of automata theory, deriving an efficient closed-form solution for the regular languages, a broad class of formal languages with many practical applications, including API calls or schema-guided JSON and YAML.

Key takeaways

• Automata theory offers elegant solutions for constraining LM output to adhere to formal languages.
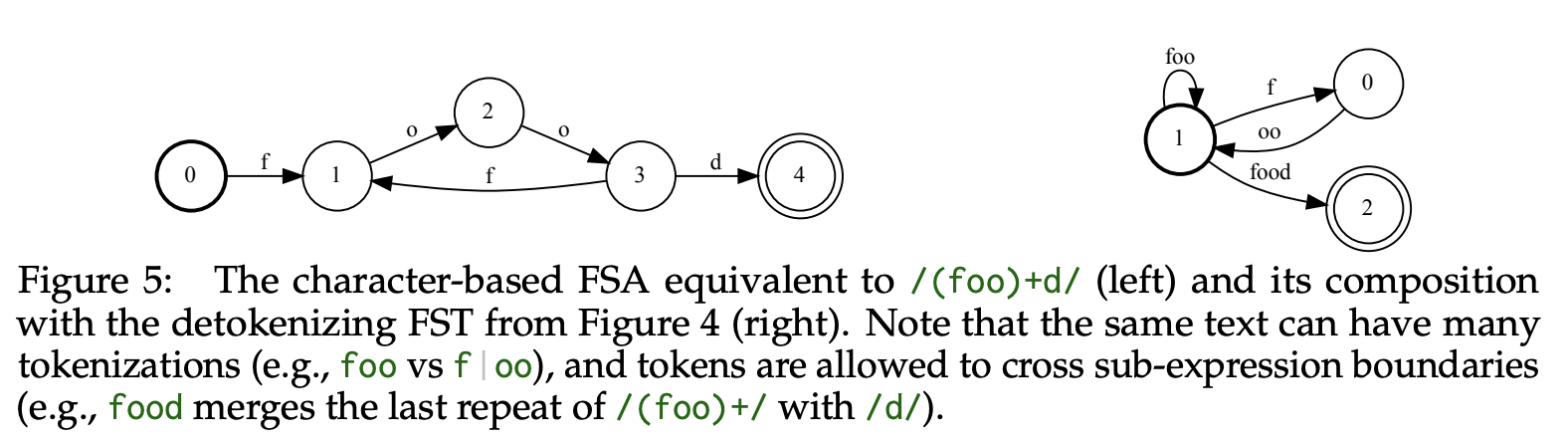
• The paper introduces a method to reformulate detokenization as a finite-state transducer (FST). This enables the adaptation of any finite-state automaton (FSA) or push-down automaton (PDA) from character-level to token-level constraints.
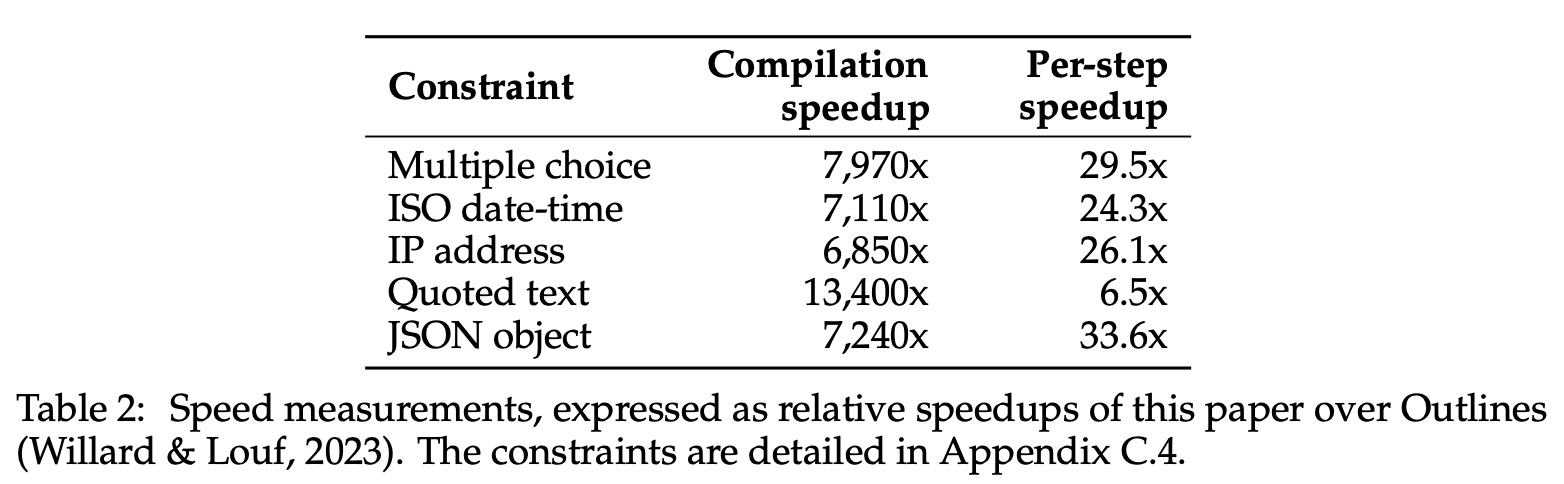
• The proposed system leverages FST composition to efficiently and correctly combine constraints with LM tokenization, resulting in significant speed improvements compared to existing methods.
• The system is extensible, allowing for the incorporation of different detokenization schemes and constraint automata.
• The approach supports both regular languages, defined by regular expressions, and deterministic context-free languages, defined by deterministic context-free grammars.
• Practical applications are demonstrated for generating JSON expressions adhering to schemas and Python dataclasses.
• The system’s efficiency makes it suitable for integration with speculative decoding, a technique for speeding up LM inference.

Experiment

Preliminary concepts

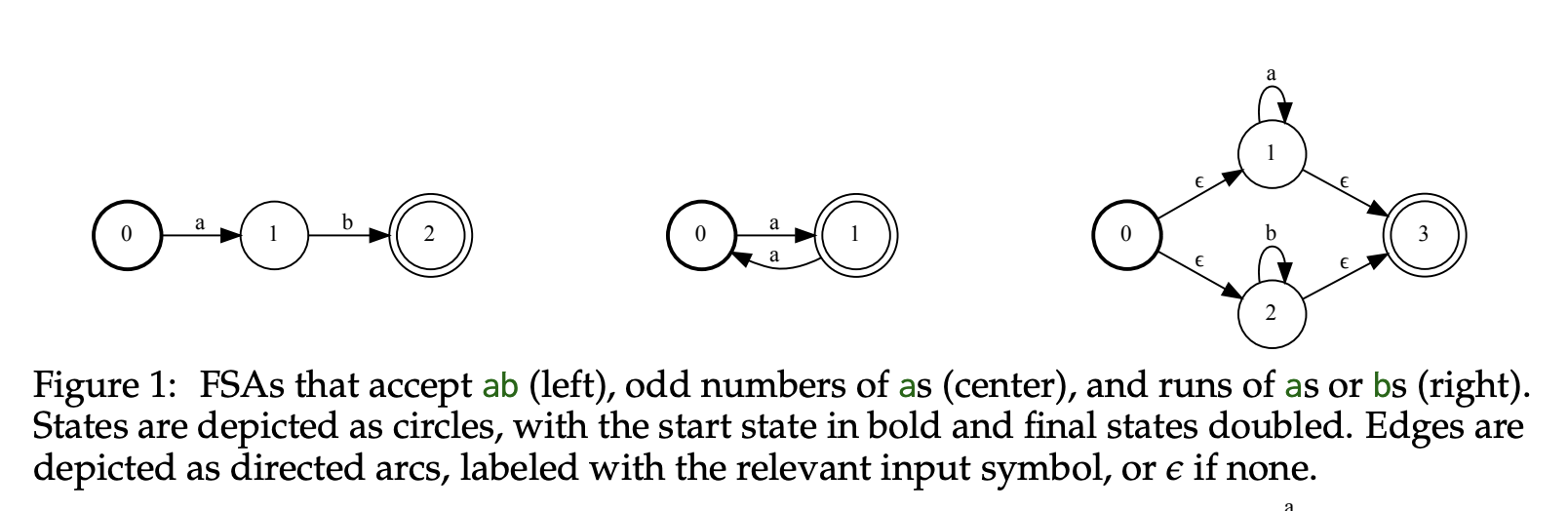
• Finite-state automata (FSAs): FSAs are computational models represented as directed graphs with states and transitions. They can accept or reject input strings based on whether a valid path through the graph exists. Regular expressions can be compiled into FSAs.
• Finite-state transducers (FSTs): FSTs are similar to FSAs but also produce output strings based on the input and the transitions taken. They are particularly useful for tasks like translation or detokenization.
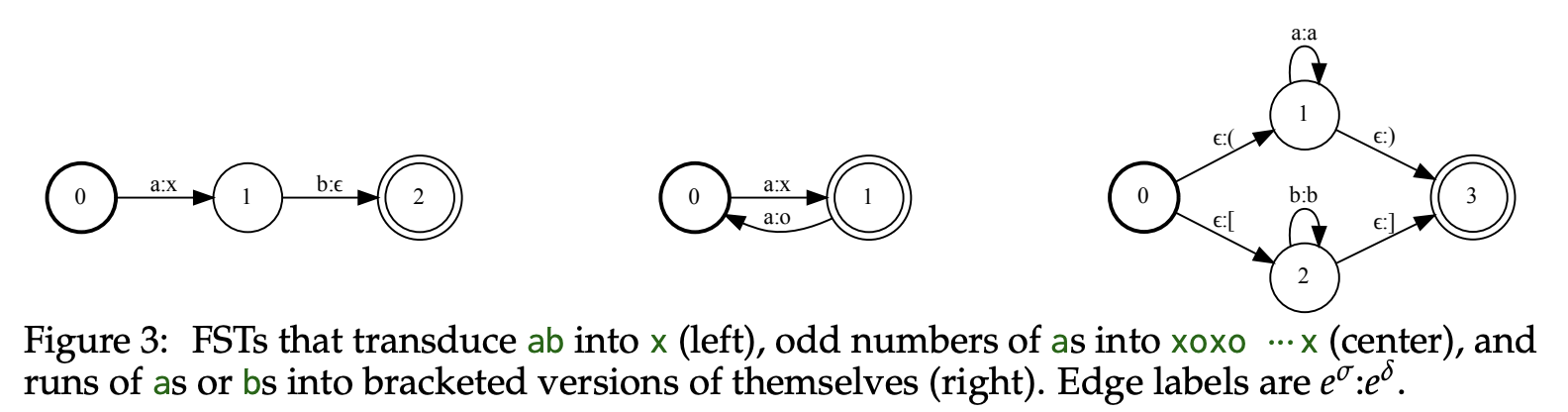
• Push-down automata (PDAs): PDAs extend FSAs with a stack, enabling them to recognize context-free languages, a broader class of languages that includes most programming language syntax.
• FST composition: FSTs can be combined sequentially, where the output of one FST becomes the input of another. This allows for modular construction of complex transformations.
• Deterministic vs. Non-Deterministic Automata: Deterministic automata have at most one valid transition for any given input symbol and state, while non-deterministic automata can have multiple. Deterministic automata are generally more efficient to process.

Results

One general recipe for applying constraints to any LM is to mask the decoder logits:

1. Based on the current state of the constraint, build a mask of valid next tokens.
2. Penalize the sampling logits using the mask, so only valid tokens are considered.
3. Feed the selected token back to the constraint, to update its state for the next step

Hence a method to force an LLM to follow constrain output:

1. Detokenization as transduction : a reformulation of detokenization (i.e., the process of converting token sequences back into text) as an FST.
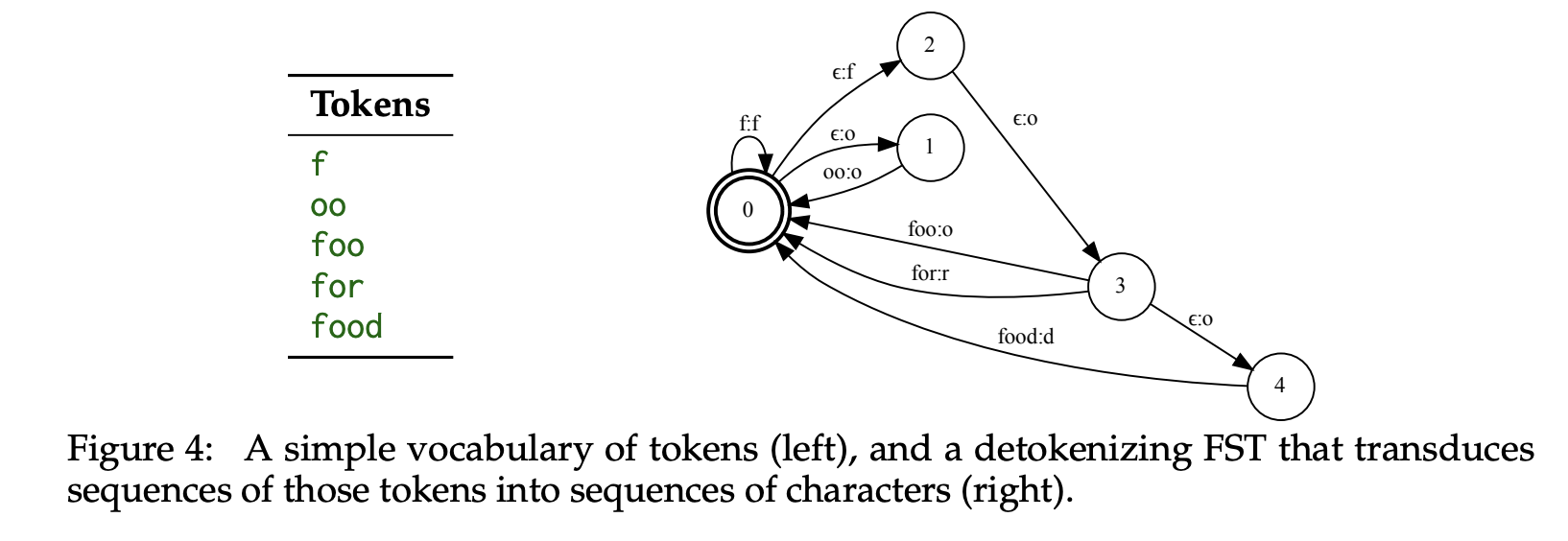
2. Adapting regular expressions to tokens : a generic method for adapting any FSA from characters to tokens. Specifically, given a token vocabulary V and an FSA A that accepts character sequences, A′ = A ◦ TV accepts essentially the same language as A, but in token form.