Learning without training:The implicit dynamics of in-context learning

Abstract

Large Language Models (LLMs) have a striking ability to learn new patterns at inference time purely from examples provided in a prompt, a phenomenon known as In-Context Learning (ICL). The underlying mechanisms that enable this “learning without training” are still largely unknown. This study investigates how the standard transformer architecture, specifically the stacking of a self-attention layer with an MLP, allows the model to implicitly modify the MLP layer’s weights based on the provided context. The paper aims to demonstrate, through both theory and experimentation, how this internal dynamic may be the reason LLMs can perform ICL.

Key takeaways

• The paper introduces the “contextual block,” a generalization of a transformer block, which consists of a contextual layer (like self-attention) stacked with a standard neural network (like an MLP).
• The central finding is that a contextual block’s output for a token with a given context is identical to its output without that context, provided the neural network’s weight matrix is updated by a specific low-rank matrix derived from the context.
• An explicit formula is provided for this implicit, low-rank weight update ($\Delta W$), which effectively transfers information from the prompt’s context into the MLP’s weights.
• The sequential consumption of context tokens creates an implicit learning dynamic that, as the paper shows, is analogous to a form of stochastic gradient descent optimization on the neural network’s weights.

Experiment

Preliminary concepts

• Contextual Layer ($A$):

A generalization of a self-attention layer. It’s defined as a network layer that can take a single vector $x$ as input (outputting $A(x)$) or, optionally, take $x$ along with a context $C$ (outputting $A(C,x)$).

• Contextual Block ($T_W$):

A generalization of a transformer block. It is the composition of a contextual layer $A$ with a neural network $M_W$ (e.g., an MLP)

$$T_W=M_W\circ A$$

• Main Theorem (Theorem 2.2):

The paper’s core theoretical claim. It states that the effect of a portion of the context, $Y\subset C$, on an input $x$ can be perfectly transferred into the weights of the neural network $M_W$. The theorem is expressed as:

$$T_W(C,x)=T_{W+\Delta W(Y)}(C\backslash Y,x)$$

The implicit weight update $\Delta W(Y)$ is a rank-1 matrix given by the formula:

$$\Delta W(Y)=\frac{(W\Delta A(Y))A(C\backslash Y,x{)}^T}{||A(C\backslash Y,x)|{|}^2}$$

where $\Delta A(Y)=A(C,x)-A(C\backslash Y,x)$ is the “context vector” associated with $Y$.

• Implicit Learning Dynamics (Proposition 3.1):

The paper shows that the sequential processing of context tokens $C=[c_1,...,c_n]$ generates a sequence of weight updates $W_1,...,W_n$. This iterative process can be realized as a form of stochastic gradient update:

$$W_i=W_{i-1}-h{\nabla }_W{L}_i(W_{i-1})$$

with :

• learning rate $h=\frac{1}{||A(x)|{|}^2}$
• loss $L_i=trace({\Delta }_i^{T}W)$ depends on the token $c_i$
• ${\Delta }_i=W_0(A(c_1,...,c_i,c_x)-A(c_1,...,c_{i+1},x))A(x{)}^T$

Objectives

The primary objectives of the experiments are to:

• Experimentally verify Theorem 2.2: demonstrate that the prediction made by a trained transformer with an in-context prompt, $T_W(C,x)$, is identical to the prediction made by the same model without the prompt but with its MLP weights modified by the calculated update $\Delta W$, $T_{W+\Delta W(C)}(x)$.
• Verify that the implicit learning dynamics converge—specifically, that the magnitude of the gradient updates ($||(\Delta W{)}_{i+1}-(\Delta W{)}_i|{|}_2$) vanishes as more context tokens are processed.
• Compare the loss trajectory of this implicit $\Delta W$ update process against a standard finetuning (GD) process using gradient descent.

Setup

• Task:
  • use an in-context regression task where the model must learn an unseen linear function $h(x)=⟨w,x⟩$ from a prompt containing input-output examples $(x_i,h(x_i))$. This setup follows previous work.
• Models:
  • A “simple transformer” with a “standard single transformer block”. The experiments verifying the theorem 2.2 and convergence explicitly use a block without the MLP skip connection.
• Datasets:
  • Prompts are generated by sampling inputs $x_i$, a query $x_{query}$, and the function weights $w$ from a standard normal distribution $\mathcal{N}(0,I_d)$. The outputs $h(x_i)$ are then computed from $h(x_i)=⟨w,x_i⟩$. For the finetuning (GD) comparison, the dimension $d=2$ and the number of examples $N=50$.
• Hyperparameters:
  • For the finetuning (GD) comparison, standard stochastic gradient descent was used with a learning rate of 0.01 and a batch size of 1. Only the MLP weight matrix was updated during this finetuning.
• Metrics:
  • Validation Loss: The mean squared error between the model’s prediction $\hat{y}(x_{query})$ and the true label $h(x_{query})=⟨w,x_{query}⟩$.
  • Convergence Metric: The L2-norm of the difference between successive weight updates, $||(\Delta W{)}_{i+1}-(\Delta W{)}_i|{|}_2$, which corresponds to the gradient update norm in Proposition 3.1.
• Customizations: The key experimental customization is the direct comparison between two prediction methods:
  • Standard ICL: The model output $T_W(C,x)$ given the full context $C$ and query.
  • Implicit Update: The model output $T_{W+\Delta W}(x)$ given only the query $x$, but after its weights $W$ have been modified by the calculated $\Delta W$ from Equation (8).

Results

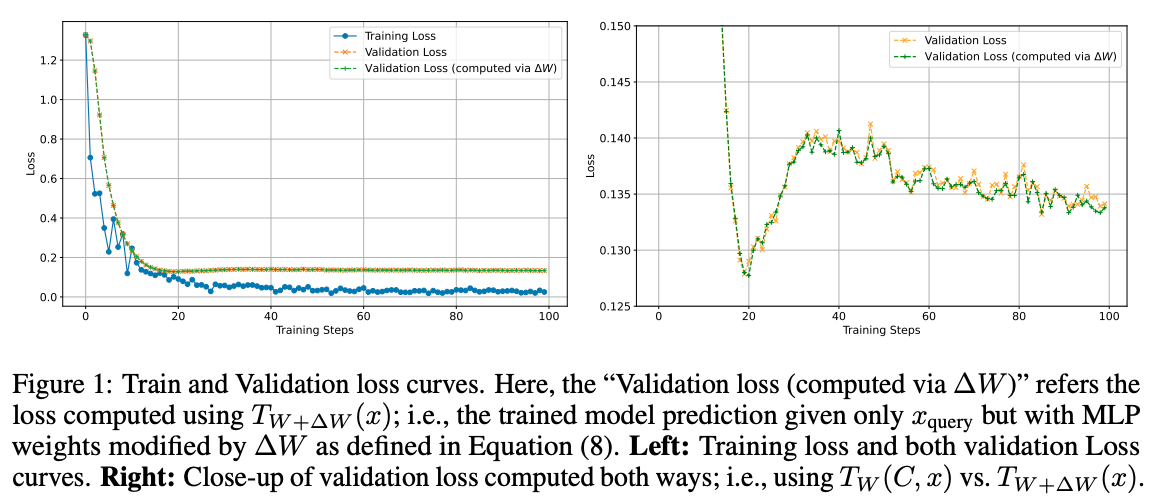
• Verification of Theorem 2.2 (Figure 1): The experiment successfully validates the main theorem. The validation loss computed using the standard in-context prompt ($T_W(C,x)$) and the loss computed using the implicit weight update ($T_{W+\Delta W}(x)$) are in “remarkable agreement”. Figure 1 (left and right) plots both validation loss curves over training steps, showing they are visually indistinguishable.
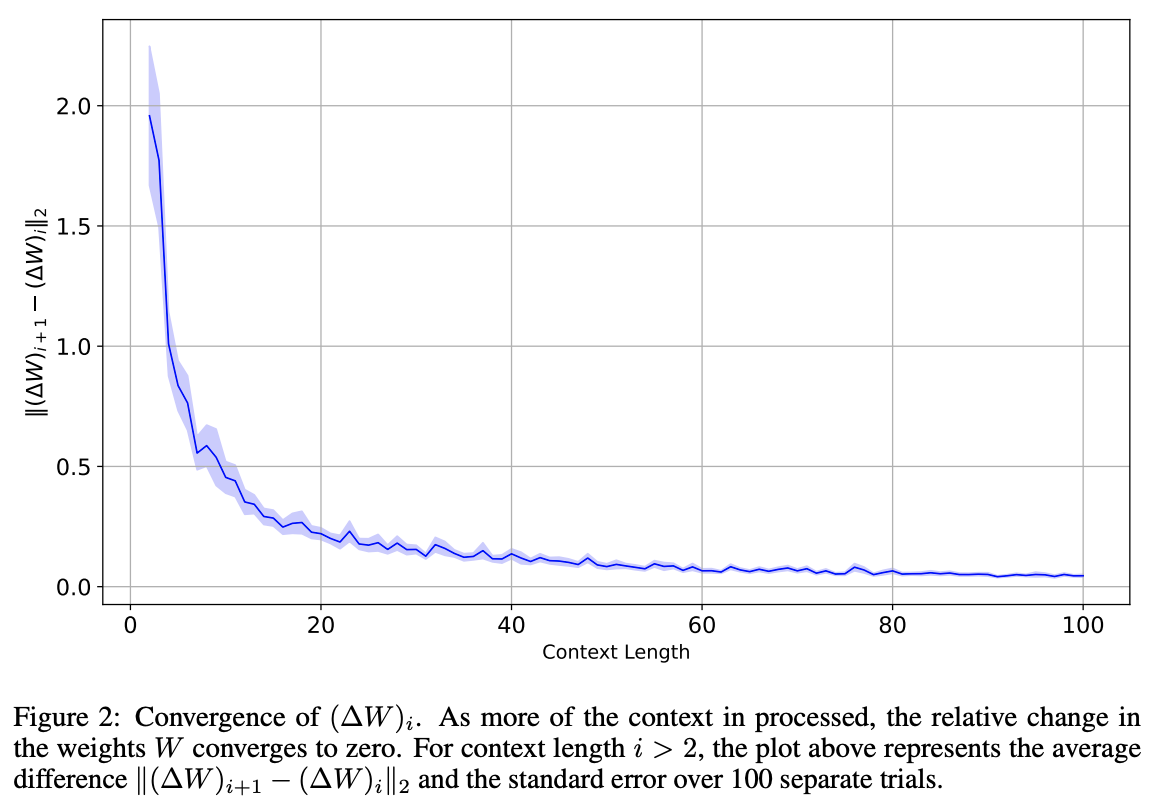
• Convergence of Implicit Dynamics (Figure 2): The implicit learning dynamics converge as predicted. Figure 2 plots the L2-norm of the marginal change in the weight update ($||(\Delta W{)}_{i+1}-(\Delta W{)}_i|{|}_2$) against the context length. This value, representing the gradient update, rapidly decreases and “vanishes” as more context tokens are processed, mimicking a converging gradient descent process.
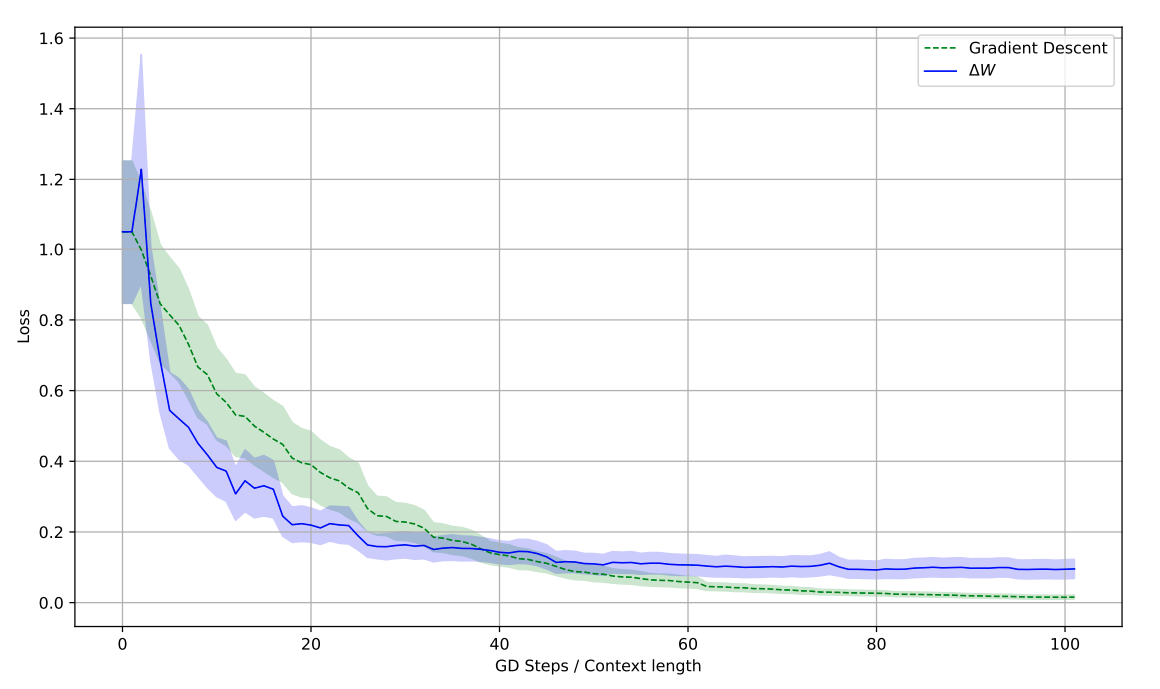
• Comparison with Finetuning (Figure 3): The implicit $\Delta W$ weight transfer and explicit finetuning via gradient descent (GD) show similar, though not identical, behaviors. Figure 3 plots the test loss for both methods against the number of examples (context length for $\Delta W$, GD steps for finetuning). Both curves show the loss decreasing as more examples are processed, with the authors noting that the two processes “minimize the loss in similar ways”.

Discussions

• Strengths:
  • The primary strength is that this theoretical framework does not require restrictive assumptions about the self-attention layer’s architecture (like linear attention), which was a major limitation of previous works.
  • The findings are general and remain valid if the self-attention layer is replaced by other types of contextual layers, such as an RNN or a Griffin block.
  • The work suggests ICL is less about the specific mechanism of self-attention and more about a fundamental “deep property” of neural networks: their ability to transfer modifications in the input space to their weight structure.
• Weaknesses (Limitations):
  • The entire derivation is valid only for a single transformer block.
  • The analysis only quantifies the context’s effect on the output of the last input token (i.e., the first generated token) .
  • It “does not capture the full mechanics of generation” beyond that single step.

• Future work:
  • The authors suggest it would be interesting to evaluate the “generative power” of different contextual layers (e.g., self-attention, RNNs) by analyzing the “usefulness” of the implicit weight modifications they produce, as defined by the paper’s formula.