The illusion of thinking: understanding the strengths and limitations of reasoning models via the lens of problem complexity

Abstract

This paper investigates the true reasoning capabilities and limitations of the latest generation of Large Reasoning Models (LRMs), which are language models designed to generate explicit thinking steps before producing an answer. The authors argue that current evaluation methods, which primarily rely on final answer accuracy on standard benchmarks, are insufficient due to issues like data contamination and their inability to provide insights into the quality of the models’ reasoning processes. To address these gaps, the paper proposes a systematic investigation using controllable puzzle environments. This approach allows for the precise manipulation of problem complexity while enabling a detailed analysis of both the final answers and the internal reasoning traces, offering a deeper look into how these models “think”.

Key takeaways

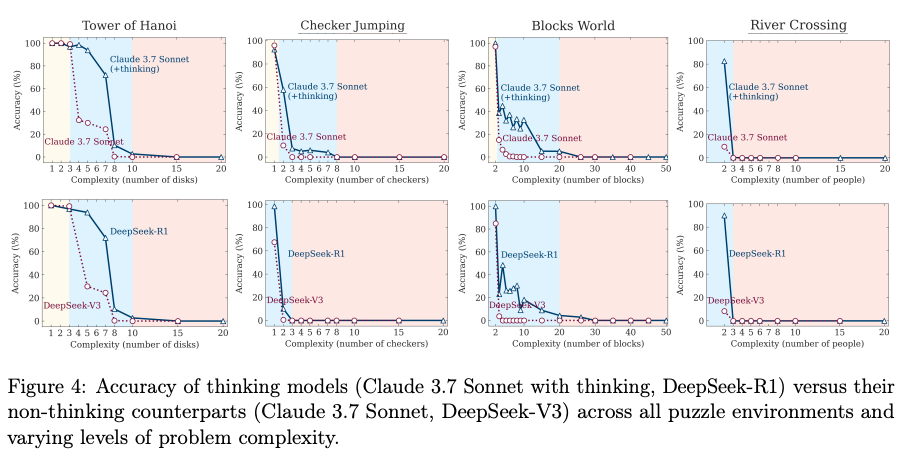
• LRMs fail to solve problems beyond a certain complexity threshold, with their accuracy collapsing to zero across various tasks.
• LRMs exhibit a counterintuitive scaling limit: their reasoning effort, measured in tokens, increases with problem complexity only up to a point before declining, even when more computational budget is available.
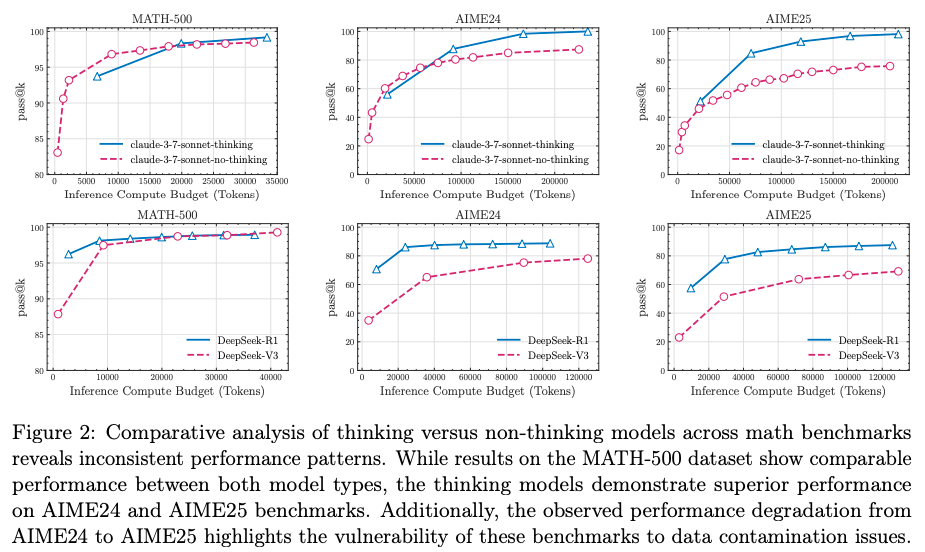
• When compared to standard Large Language Models (LLMs) with an equivalent computational budget, a three-tiered performance pattern emerges: standard LLMs perform better on low-complexity tasks, LRMs have an advantage on medium-complexity tasks, and both fail on high-complexity tasks.
• LRMs demonstrate significant limitations in exact computation, as their performance does not improve even when explicitly provided with the correct algorithm to solve a problem.
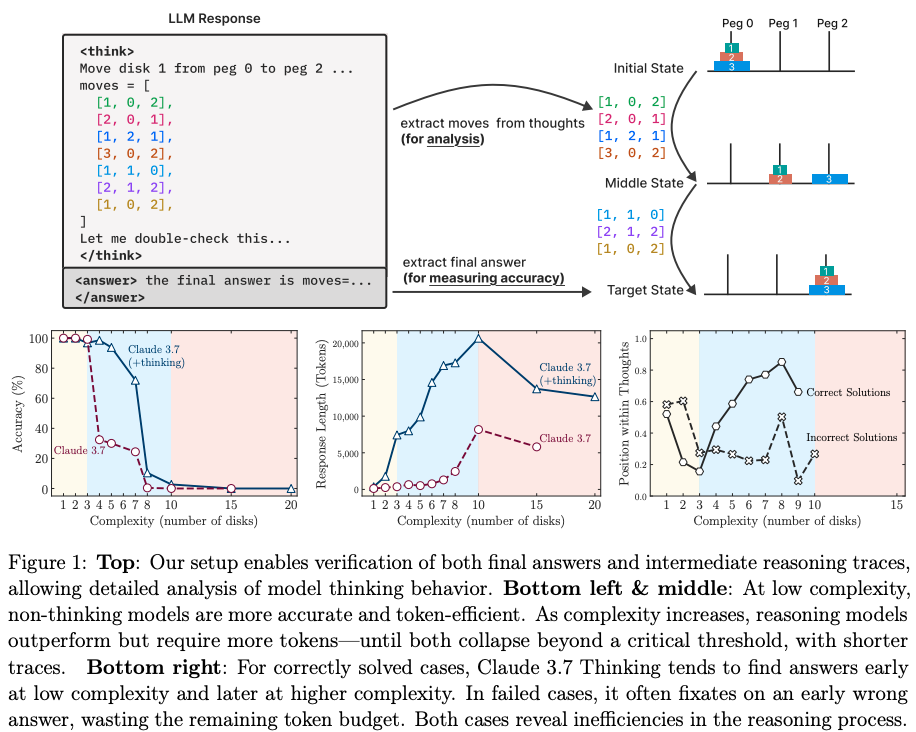
• Analysis of the models’ “thoughts” reveals that for simple problems, LRMs often find the correct solution early but continue to explore incorrect paths, a phenomenon described as “overthinking”.
• LRMs show inconsistent reasoning abilities across different puzzle types, sometimes solving problems requiring hundreds of steps while failing on others that require far fewer, suggesting a reliance on memorized patterns rather than generalizable problem-solving skills.

Experiment

Objectives

The primary objectives of the experiments are :

• to systematically evaluate the strengths and limitations of LRMs by precisely controlling for problem complexity.
• to move beyond final answer accuracy and analyze the structure, quality, and patterns within the internal reasoning traces (“thoughts”) of these models.
• to conduct a fair comparison between LRMs and their non-thinking standard LLM counterparts by providing them with an equivalent inference compute budget.
• to challenge and highlight the limitations of the current evaluation paradigm, which relies on established mathematical benchmarks that may suffer from data contamination and do not allow for controlled experimentation.

Setup

Detail the specific experimental configurations, including:

• Models:
  • Claude 3.7 Sonnet (with and without thinking).
  • DeepSeek-R1 (a reasoning model) and DeepSeek-V3 (its standard counterpart).
  • For final accuracy experiments, OpenAI’s o3-mini (medium and high configurations) were also included.
• Datasets: Four puzzles environments:
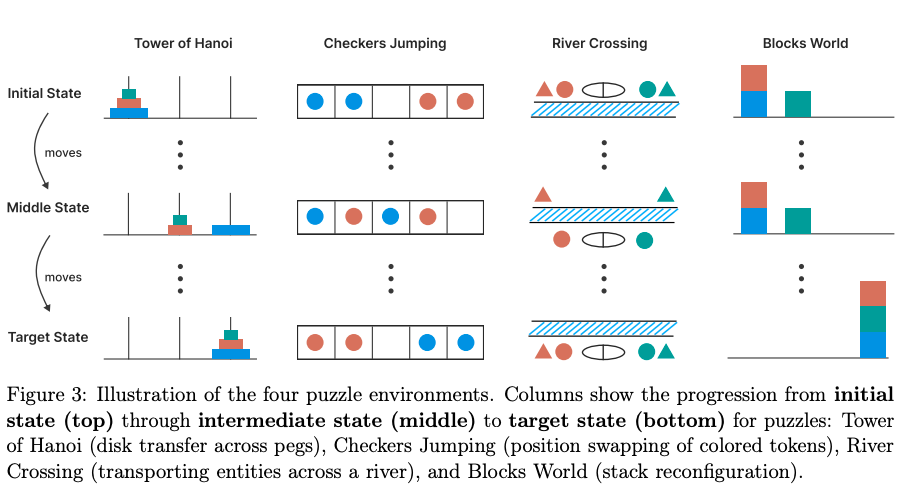
  • Tower of Hanoi is a puzzle featuring three pegs and n disks of different sizes stacked on the first peg in size order (largest at bottom). The goal is to transfer all disks from the first peg to the third peg. Valid moves include moving only one disk at a time, taking only the top disk from a peg, and never placing a larger disk on top of a smaller one. The difficulty in this task can be controlled by the number of initial disks as the minimum number of required moves with $n$ initial disks will be $2^n-1$.
  • Checker Jumping is a one-dimensional puzzle arranging red checkers, blue checkers, and a single empty space in a line. The objective is to swap the positions of all red and blue checkers, effectively mirroring the initial configuration. Valid moves include sliding a checker into an adjacent empty space or jumping over exactly one checker of the opposite color to land in an empty space. No checker can move backward in the puzzle process. The complexity of this task can be controlled by the number of checkers: with $2n$ checkers, the minimum number of moves required will be $(n+1{)}^2-1$.
  • River Crossing is a constraint satisfaction planning puzzle involving n actors and their corresponding n agents who must cross a river using a boat. The goal is to transport all $2n$ individuals from the left bank to the right bank. The boat can carry at most k individuals and cannot travel empty. Invalid situations arise when an actor is in the presence of another agent without their own agent present, as each agent must protect their client from competing agents. The complexity of this task can also be controlled by the number of actor/agent pairs present. For $n=2$, $n=3$ pairs, boat capacity of $k=2$ was used and for larger number of pairs $k=3$.
  • Blocks World is a block-stacking puzzle requiring rearrangement of blocks from an initial configuration into a specified goal configuration. The objective is to find the minimum number of moves needed for this transformation. Valid moves are restricted to the topmost block of any stack, which can be placed either on an empty stack or on top of another block. The complexity in this task can be controlled by the number of blocks present.
• Hyperparameters:
  • For Claude 3.7 Sonnet and DeepSeek models, a maximum token budget of 64k was allowed.
  • Temperature = 1.0 for all API-based model.
  • For each puzzle at every complexity level, 25 samples were generated to report average performance.
• Metrics:
  • For each puzzle instance, 25 i.i.d samples were generated and then accuracy reported.
  • A global pass@k ($k=25$) using the generated samples of thinking and non-thinking across all task is reported for equivalent compute budgets.

Results

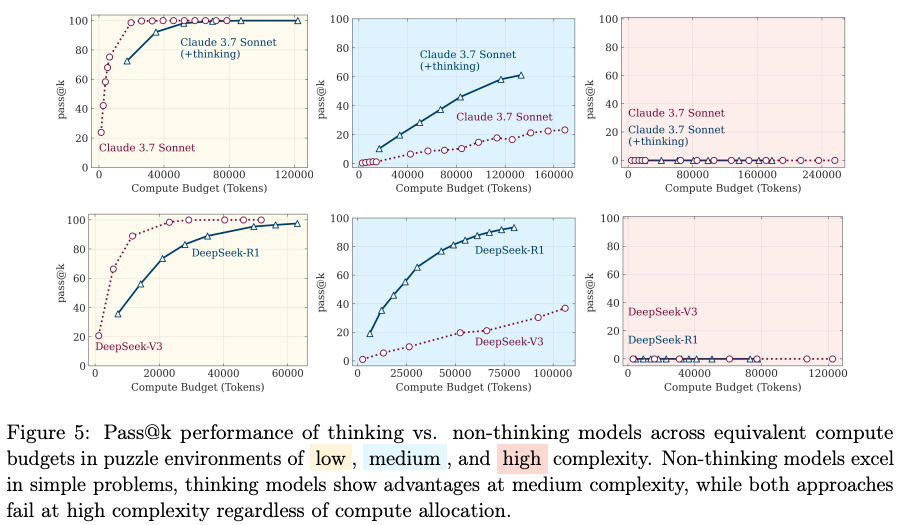
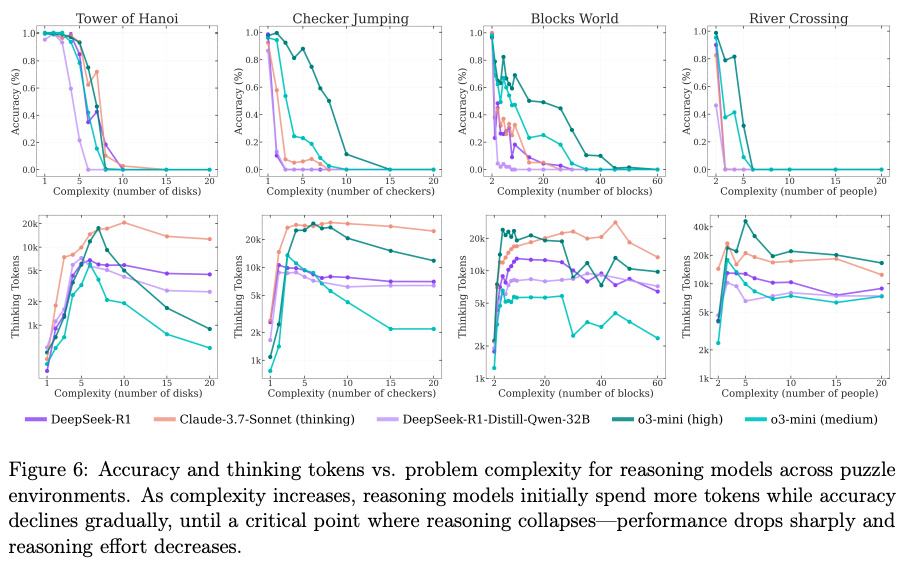
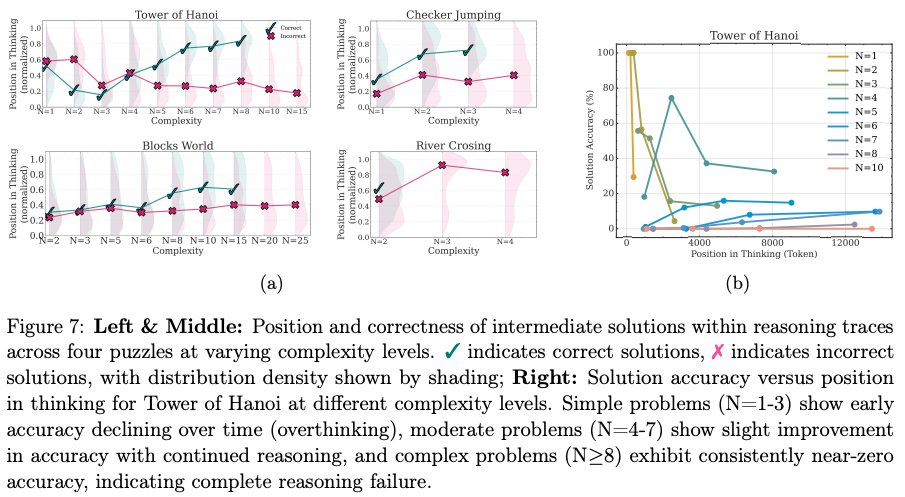
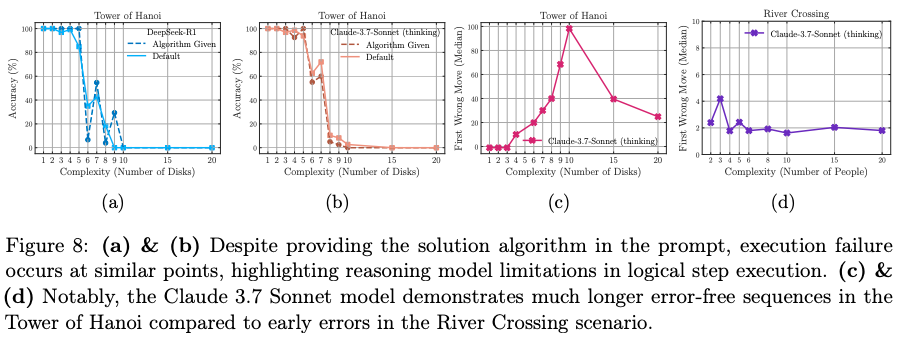
Discussions

• Taking a look at the prompt for each puzzle, we can observe that the choice of representation of each step is not explicit (for verification purpose, the model is tasked to return the stack of move at each step rather than the state of the game). This has several implications:
  • Increased Cognitive Load and Lack of Intermediate Grounding: By asking for a final list of moves, the experiment forces the model to perform all state-tracking internally. It must mentally simulate the entire puzzle from start to finish to produce the correct action sequence. This is a much harder task than reasoning step-by-step, where the model can generate a move, observe the new state, and then decide on the next move. Without being prompted to write down the intermediate states, the model has no “scratchpad” to ground its reasoning, making it more prone to error.
  • Hindrance to Self-Correction: The paper places importance on analyzing self-correction mechanisms within the reasoning traces. However, a format that only lists moves makes self-correction incredibly difficult. An illegal move (e.g., placing a large disk on a smaller one ) is not immediately obvious from the move list [1, 0, 2] alone; its invalidity only becomes apparent when one simulates the state. If the model were prompted to output the resulting state after each move, an invalid state would serve as a direct and explicit error signal that the model could potentially identify and correct in its next thought process.
  • Encourages Pattern Matching over Deliberate Planning: The chosen format may inadvertently test pattern matching rather than true step-by-step reasoning. A model that has seen many Tower of Hanoi solutions in its training data might simply output a memorized sequence of moves. It doesn’t necessarily need to “reason” about the state changes. This could explain the surprising results where models succeed at puzzles with long solutions (Tower of Hanoi) but fail at puzzles with shorter, more complex constraints (River Crossing). The former is a common, well-documented algorithm, while the latter might be less prevalent in web data.
• Those models are multimodal, the experiment would have been closer to their actual capacities if it provides the models a way to see the flow of resolution. Puzzles like the Tower of Hanoi, Blocks World, and Checker Jumping are fundamentally spatial. Humans often solve them by visualizing the state of the board or pegs. A text-based representation like [[‘A’, ‘B’], [‘C’, ‘D’], []] is an abstract and less intuitive way to represent a physical arrangement compared to an image. The paper itself uses diagrams to explain the puzzles to the reader, tacitly acknowledging the value of visual aids, yet this advantage is not extended to the models being tested.

The X user @scaling01 made several excellent points about this experimentation:

The paper’s conclusion about a “reasoning collapse” in the Tower of Hanoi puzzle may be misleading, as it overlooks a critical mechanical constraint: the models’ maximum output token limits.

• Mechanical Failure vs. Reasoning Collapse: The Tower of Hanoi puzzle with N disks requires a minimum of $2^n-1$ moves to solve. The prompt requires an output format of moves = [[disk, from_peg, to_peg], …], which costs approximately 10 tokens per move. The paper states that the DeepSeek and Claude models were run with a maximum length of 64k tokens. - For $n=12$, the solution requires $2^{12}-1=4,095$ moves, which would be over 40,000 tokens, already pushing the limits of the models. - For $n=13$, the solution requires $2^{13}-1=8,191$ moves, demanding over 80,000 tokens, which exceeds the stated context window for these models. Therefore, the perfect accuracy collapse observed for all models beyond a certain number of disks (as seen in Figure 6) is not necessarily a failure of reasoning. It is, at least in part, a mechanical failure, as the models physically cannot generate the complete required output.
• Model Behavior Aligns with This Constraint: As @scaling01 points out, the models themselves appear to recognize this limitation. The paper’s finding that models “counterintuitively begin to reduce their reasoning effort” at high complexity could be interpreted as the model recognizing that the full solution is too long to generate and “giving up” on the task, rather than a fundamental collapse in its reasoning capability.
• The Compounding Probability of Error: For exponentially long solutions, even a minuscule probability of error at each step will compound, making a perfect output statistically improbable. A model could have a flawless understanding of the algorithm but still fail on a 32,767-step problem due to the sheer number of opportunities to make a single token-level mistake. This is an issue of probabilistic execution, not necessarily logical reasoning.

The paper’s central argument that models “struggle with puzzles of lower compositional depth while succeeding on different puzzles with higher compositional depth” is based on a flawed premise, as it equates solution length with reasoning difficulty.

• Solution Length is Not Reasoning Difficulty: The paper defines “compositional depth” as the number of moves in the optimal solution. However, as @scaling01 argues, the length of a solution does not determine how difficult it is to find that solution. The complexity of a problem is better measured by the size of the search space and the difficulty of navigating its constraints.
• The Logical Simplicity of Tower of Hanoi: Although the Tower of Hanoi has an exponentially long solution, the underlying logic is simple and deterministic. There is a well-known recursive algorithm that requires no complex search or backtracking; at each valid step, there is effectively only one correct move to make to stay on the optimal path. The models have likely learned this simple, repetitive algorithm from their training data.
• The Higher Reasoning Demand of Other Puzzles: In contrast, puzzles like River Crossing and Blocks World, while having shorter solutions, are logically more complex. - River Crossing requires satisfying multiple overlapping constraints simultaneously (e.g., “no actor can be in the presence of another agent… unless their own agent is also present” ), which demands careful planning and state-checking. - Blocks World requires true lookahead planning, as moves made now can block necessary future moves, often requiring backtracking or finding a complex path to un-stack certain blocks. The reasoning difficulty of these puzzles is therefore higher, as they require navigating a complex search space of possible (but mostly invalid) moves.
• Reinterpreting the Paper’s “Puzzling Behavior”: The paper presents the models’ varying performance across puzzles as a puzzling phenomenon (Figure 10). However, if we re-rank the puzzles by their actual reasoning difficulty (River Crossing > Blocks World > Checker Jumping > Tower of Hanoi), the models’ performance aligns perfectly with this ranking. They perform best on the logically simplest task (Tower of Hanoi) and worst on the most constraint-heavy one (River Crossing). Thus, the “puzzling behavior” is not a puzzle at all; it is an artifact of the paper’s flawed metric for complexity. The results simply show that the models are better at executing simple, repetitive algorithms than they are at complex, constraint-based planning.