Abstract
Training on high-quality synthetic data from strong language models (LMs) is a common strategy to improve the reasoning performance of LMs. In this work, we revisit whether this strategy is compute-optimal under a fixed inference budget (e.g., FLOPs). To do so, we investigate the trade-offs between generating synthetic data using a stronger but more expensive (SE) model versus a weaker but cheaper (WC) model.
Key takeaways
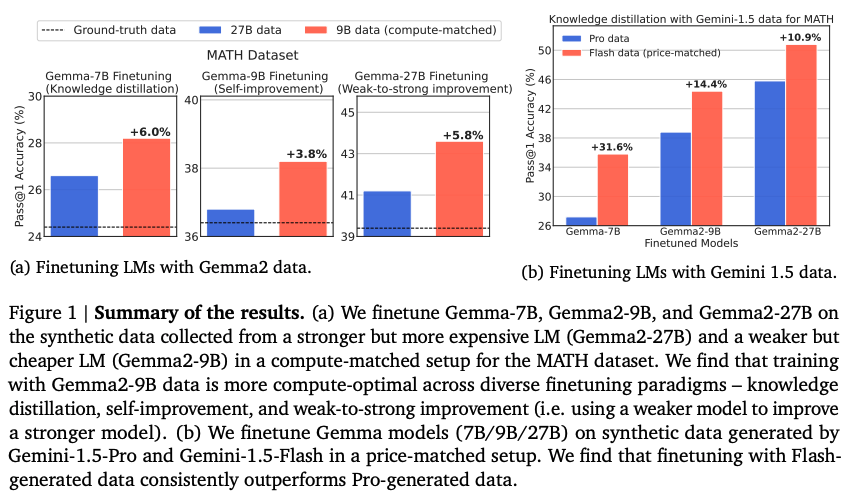
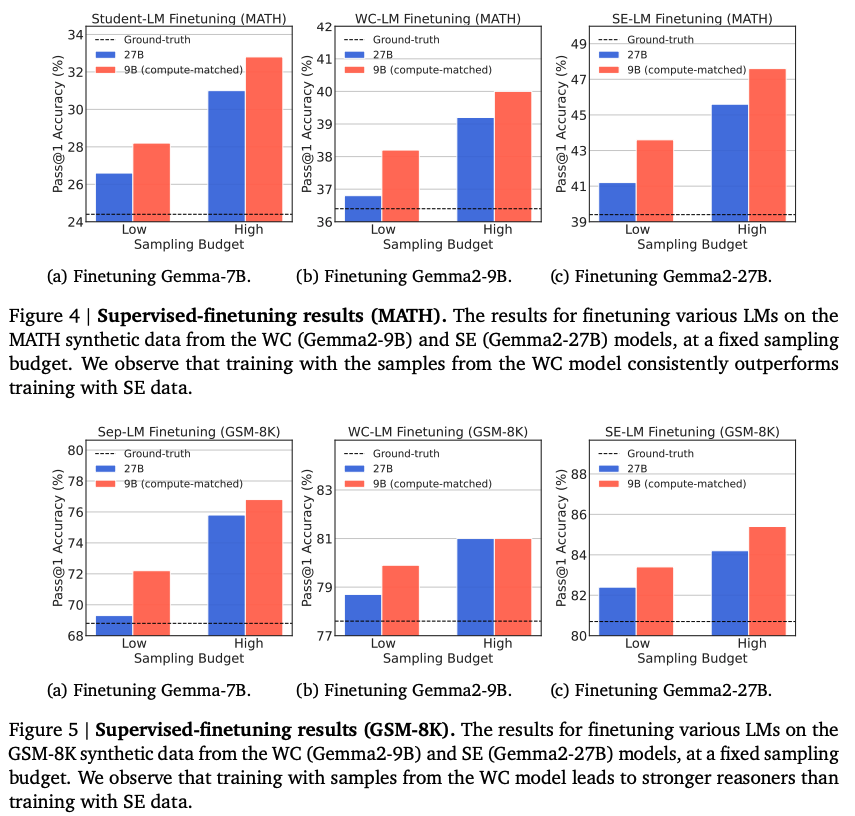
- Contrary to common-practice, training language models with synthetic data generated by WC models is more compute-optimal than using data from SE models.
- This holds true across different fine-tuning paradigms like knowledge distillation, self-improvement, and a novel “weak-to-strong improvement,” where a weaker model is used to improve a stronger one.
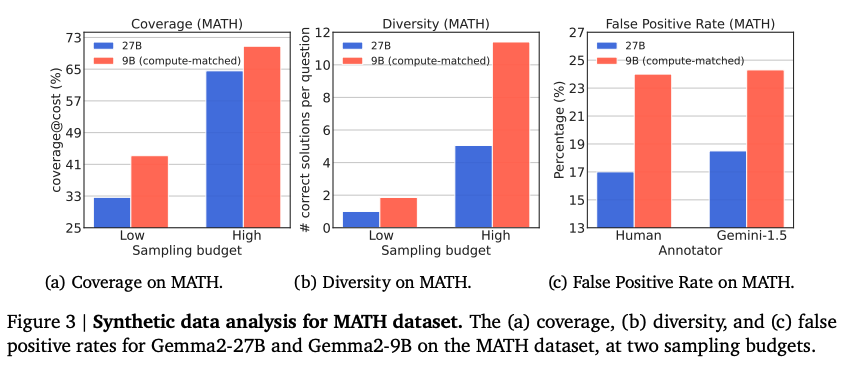
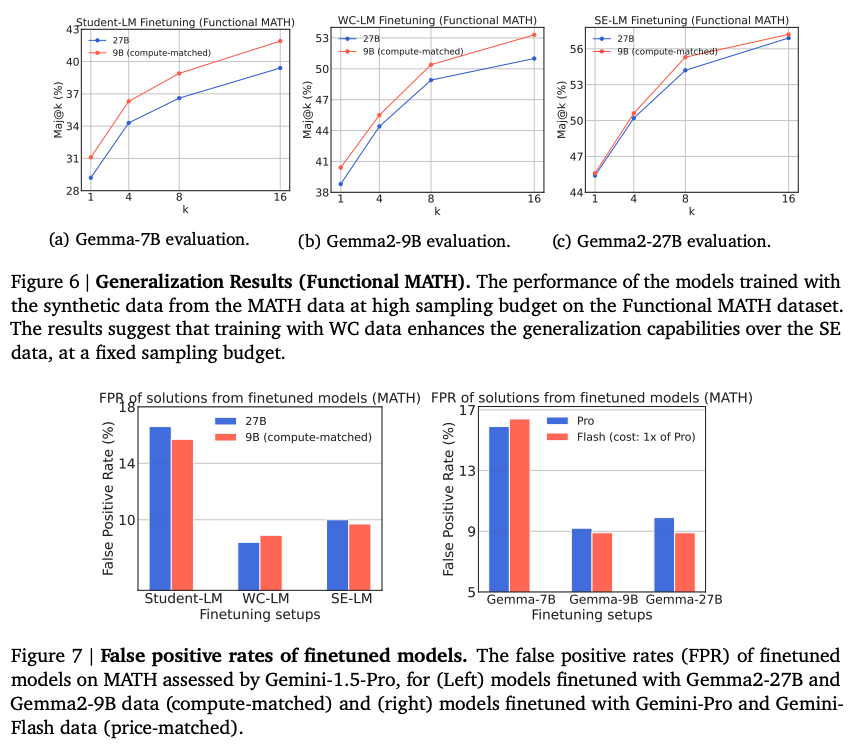
- WC models achieve higher coverage and diversity in their generated data compared to SE models under a fixed compute budget. However, WC data may have a higher false-positive rate (incorrect reasoning despite a correct final answer). Despite this, models fine-tuned on WC data show comparable or even lower false-positive rates than those trained on SE data.
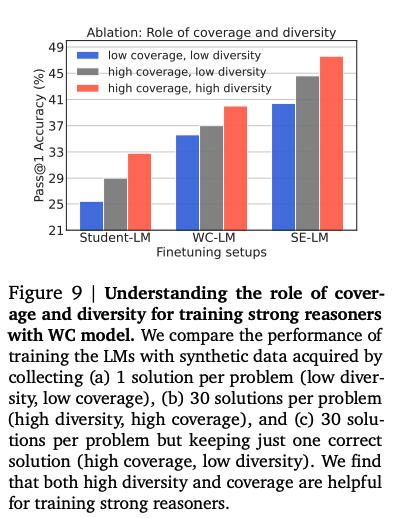
- Both coverage and diversity are crucial for good performance: models trained on datasets with high coverage and high diversity consistently outperformed those trained on datasets with only high coverage or high diversity.
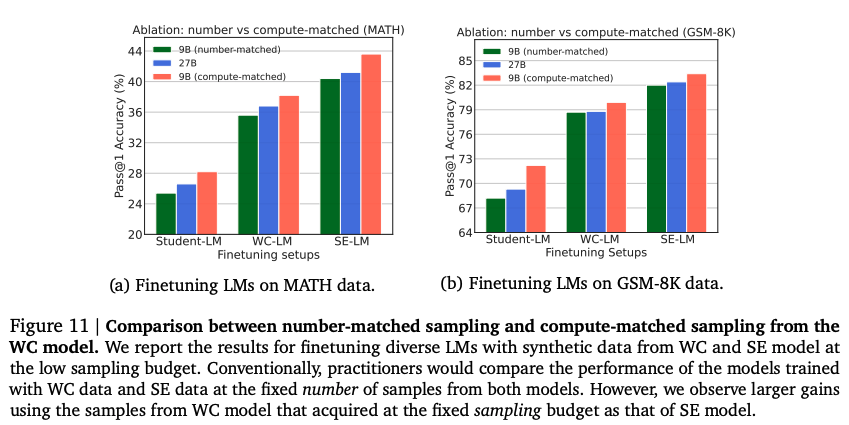
- Compute-matched sampling is superior to number-matched sampling: models trained with compute-matched WC data performed significantly better than those trained with number-matched WC data.
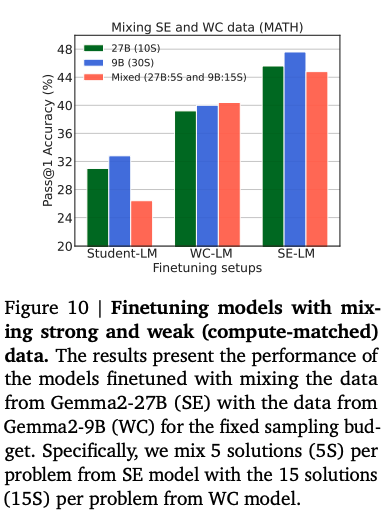
- Mixing WC and SE data might not always be beneficial: in some cases, it even led to slightly worse results compared to using only WC or SE data. This indicates that data mixing might be context-dependent and requires further investigation.
- The trend of smaller language models improving faster than larger ones suggests that this approach will become increasingly relevant in the future.
Experiment
Preliminary concepts
-
Leverage reasoning datasets:
- let be a training dataset of size 𝑛 with reasoning questions and final answers
- sample multiple solutions for each at a non-zero temperature and create the synthetic data where 𝑘 is the number of samples, is the 𝑗-th reasoning chain (i.e. solution) generated by the model for , and is the model’s final answer for in the 𝑗-th sample.
- filter the incorrect solutions by comparing 𝑗 to and removing the solutions whose final answer do not match that of the gold answer.
- finetune a model on the remaining data .
-
Metrics :
Objectives
The primary objective of this paper is to challenge the common practice of using stronger and more expensive language models for generating synthetic data to train language model reasoners. The authors aim to demonstrate that using weaker but cheaper models for this task can be more compute-optimal. This is investigated across various fine-tuning paradigms and model families.
Setup
-
Training paradigms:
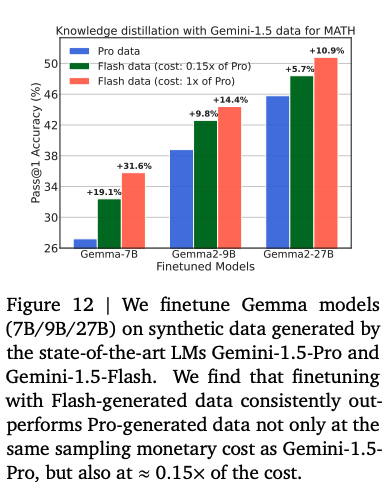
- Knowledge distillation: where a student LM learns from a teacher LM
- Self-improvement: where an LM learns from self-generated data
- Weak-to-strong improvement: a novel fine-tuning paradigm where a stronger model is improved using data generated from a weaker model.
-
Models:
- Gemma family: Gemma-7B, Gemma2-9B (WC), Gemma2-27B (SE)
- Gemini family: Gemini-1.5-Pro (SE), Gemini-1.5-Flash (WC)
- Gemini-Pro-1.5: Used as an evaluator for reasoning correctness.
-
Datasets:
- MATH: A dataset of competition-level math problems.
- GSM-8K: A dataset of grade-school-level math problems.
- Functional MATH: Used to assess generalization capabilities.
- MBPP: A coding dataset used to explore the effectiveness of the approach in coding tasks.
- HumanEval: A coding dataset used for evaluating fine-tuned models trained on MBPP.
-
Hyperparameters:
- Sampling: Top-K (K=3) strategy used for generating candidate solutions.
- Fine-tuning: Batch size 32 for Gemma2 models, batch size 8 for Gemma1-7B, various learning rates tested (1e-7, 5e-7, 1e-6), number of fine-tuning steps varied depending on the sampling budget and model size.12
-
Metrics:
- Synthetic data quality: Coverage (number of unique problems that are solved), Diversity (average number of unique solutions), False-Positive Rate (percentage of problems that arrive at the correct final answer but with a wrong reasoning).
- Fine-tuned model performance: pass@1 accuracy with temperature = 0, maj@k accuracy with temperature = 0.7.
-
Compute-matched sampling: The number of samples generated from WC and SE models are adjusted based on their compute costs to ensure a fair comparison.
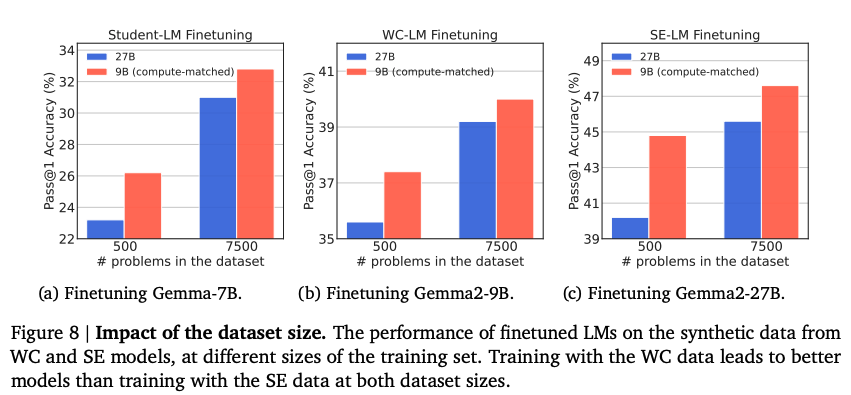
Results